遺傳算法在供熱管道直埋彎頭優化設計的應用

摘 要

摘要：采用遺傳算法對直埋水平彎頭進行優化設計。以彎頭造價最低為優化目標，采用懲罰函數法處理復雜的非線性約束，求出最優的曲率半徑和壁厚，結果可直接應用于工程設計。關鍵詞：直
摘要：采用遺傳算法對直埋水平彎頭進行優化設計。以彎頭造價最低為優化目標，采用懲
罰函數法處理復雜的非線性約束，求出最優的曲率半徑和壁厚，結果可直接應用于工程設計。
關鍵詞：直埋供熱管道；彎頭；遺傳算法；懲罰函數法
Application of Genetic Algorithm to Optimum Design of Directly Buried Elbow of Heat-supply Pipeline
WANG Chun-xiang，GUO Xiao-ni
Abstract：The optimum design of directly buried horizontal elbow is performed using genetic algorithm. Taking the lowest cost of elbow as the objective. the complex nonlinear constraints are treated using penalty function method，and the optimum curvature radius and pipe wall thickness are calculated. The results can be directly used in engineering design.
Key words：directly buried heat-supply pipeline；elbow；genetic algorithm；penalty function method
1 概述
 直埋供熱管道一般由預制保溫管、彎頭、三通、變徑管等組成，其中彎頭是重要管件之一，也是薄弱環節之一[1，2]。隨著集中供熱規模的擴大，供熱管道的管徑不斷增大，管道承受的壓力和溫度也不斷提高，對彎頭的要求也越來越高。當彎頭側臂較長、曲率半徑較小、循環溫差較大時，會導致峰值應力，發生低循環塑性變形，引起塑性破壞，造成重大損失。因此，在工程設計中我們要合理選取彎頭。在選取時主要考慮兩個參數：壁厚、曲率半徑。傳統方法是通過經驗先選出彎頭，然后把參數代入包含隱式方程的計算式，通過迭代計算來驗證是否符合要求。這種方法的不足在于無法直接求解出壁厚、曲率半徑，而且更不可能求出最經濟的壁厚和曲率半徑，只能是先選型后驗算[3，4]。為解決傳統設計選型方法無法求出最經濟的壁厚和曲率半徑的問題，本文嘗試采用遺傳算法對直埋水平彎頭進行優化設計。
    彎頭優化設計的思路和方法如下：選取彎頭壁厚、曲率半徑作為設計變量；以彎頭造價最低為優化目標；以滿足一定壽命下彎頭的疲勞強度為性能約束，將壁厚、曲率半徑作為邊界約束，建立優化設計的數學模型。鑒于所建立的模型屬于約束非線性優化問題，且含有一些復雜的隱式方程，難以判斷其是否為凸規劃優化問題。若按非凸規劃優化問題求解這樣的模型，采用傳統的約束優化方法(單點搜索)不一定能求得全局最優解，因此筆者采用了具有全局優化搜索能力的遺傳算法作為該問題的求解算法。
2 遺傳算法
    遺傳算法作為一種全局優化搜索方法，以其簡單通用、魯棒性強、適于并行處理以及應用范圍廣等特點，在求解復雜的工程優化問題中取得了良好的效果。它是基于生物進化的思想，將優化計算中的迭代過程模擬成物種進化的過程，形成一種具有“生成+檢驗”特征的搜索算法[5]。它以編碼空間代替問題的參數空間，以適應度函數為評價依據，以編碼群體為進化基礎，以對群體中個體位串的遺傳操作實現選擇和遺傳機制，建立起一個迭代過程，使遺傳算法具有了其他傳統優化方法所沒有的特性。遺傳算法的計算流程見圖1。
 

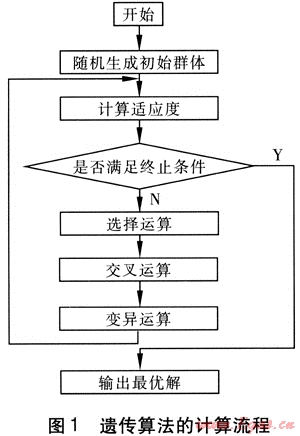
遺傳算法用于求解約束非線性最優化問題，最常用的方法是懲罰函數法，其本質是通過懲罰不可行解，把有約束的問題轉化為無約束問題。目前常用的懲罰函數法有：靜態懲罰函數法、動態懲罰函數法、退火懲罰函數法等[6]，本中采用靜態懲罰函數法[7]。這種方法對每個約束設定了三個違約水平，對每個違約水平和每個約束產生一個懲罰因子，違約水平越高，懲罰因子Rij(i=1，2，…，L；j=1，2，…，m)越大。Rij確定后，在算法的演化過程中是不變的。考慮了懲罰因子后的新適應度F(x)的表達式為：
 
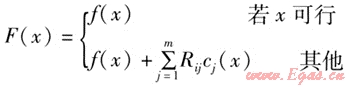
式中F(x)——考慮了懲罰因子后的新適應度
    x——設計變量
    f(x)——目標函數
    m——約束函數的數量
    Rij——懲罰因子
    cj(x)——約束函數
3 選型優化應用實例
    直埋水平彎頭見圖2，要求在滿足疲勞壽命和強度條件[3，4]的前提下進行優化選型，使壁厚和曲率半徑達到最經濟。
 

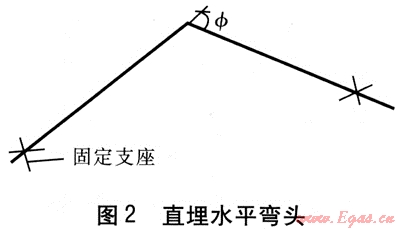
    由于直埋水平彎頭危險點處的環向應力和軸向應力都為拉應力，而徑向應力(最小主應力)近似為零，當采用第三強度理論時，彎頭處的總應力就是環向應力，它包括彎矩產生的環向應力和內壓產生的環向應力[3，4]。其中由彎矩產生的環向應力σbt的計算式為：
 
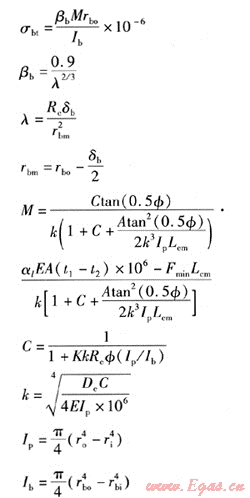
式中σbt——由彎矩產生的環向應力，MPa
    βb——彎頭平面彎曲環向應力加強系數
    M——彎頭的彎矩，N·m
    rbo——彎頭的外表面半徑，m
    Ib——彎頭鋼管的橫截面慣性矩，m4
    λ——彎頭的尺寸系數
    Rc——彎頭的計算曲率半徑，m
    δb——彎頭的公稱壁厚，m
    rbm——彎頭橫截面的平均半徑，m
    C——土壤橫向壓縮反力系數
    ф——轉角管段的折角(鄰補角)，rad
    k——與土壤特性和預制保溫管剛度有關的參數
    A——鋼管管壁橫截面面積，m2
    Ip——直管壁橫截面慣性矩，m3
    Lcm——彎頭平均計算臂長，m
    αl——鋼材的線脹系數，K-1
    E——直埋保溫管鋼管的彈性模量，MPa
    t1——直埋保溫管工作循環最高溫度，℃
    t2——直埋保溫管工作循環最低溫度，℃
    Fmin——直埋保溫管單位長度最小摩擦力，N/m
    K——彎頭鋼管的柔性系數(光滑彎管)
    Dc——預制保溫管外殼外徑，m
    ro——直埋保溫管鋼管外半徑，m
    ri——直埋保溫管鋼管內半徑，m
    rbi——彎頭鋼管的內表面半徑，m
內壓產生的環向應力σpt的計算式為：
 
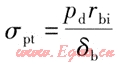
式中σpt——內壓產生的環向應力，MPa
    pd——管道的設計壓力，MPa
由以上可知，彎頭的曲率半徑Rc和公稱壁厚δb是兩個獨立的變量，也是工程中選擇彎頭的決定性參數，所以設計變量石的表達式為：
 
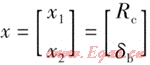
式中x1——彎頭的曲率半徑，m
    x2——彎頭的公稱壁厚，m
   從經濟性角度考慮，在滿足安全的條件下彎頭的體積越小越經濟。建立目標函數f(x)：
    f(x)=фπ[r2bo-(rbo-x2)2]x1
    采用簡化疲勞分析時，彎頭處應力的變化幅度及其強度條件可表示為：
    △σ=σbt+0.5σbt，△σ≤σall
式中△σ——彎頭處應力的變化幅度，MPa
    σall——鋼材在計算溫度下的基本許用應力，MPa
    最后得到優化目標函數為：
    minf(x)=min｛фπ[r2bo-(rbo-x2)2]x1｝
   約束條件為：
    DN≤x1≤6DN
    δmin≤x2≤0.02m
    σbt+0.5σpt-3σall≤0
式中DN——管子的公稱直徑，m
    δmin——彎頭的最小壁厚，m
    這是一個帶有不等式約束的含有兩個設計變量的優化設計問題。以規格為DN 300、400、500mm的直埋水平彎頭為例，管頂埋深為1m、熱水溫度為130℃、設計壓力為1.6MPa、ф=90°，將彎頭直臂視為無限長。求解過程如下：
    ① 參數編碼：對于二進制編碼和實數編碼，一般二進制編碼比實數編碼搜索能力強，但實數編碼比二進制編碼在變異操作上能夠保持更好的種群多樣性，因此采用實數編碼。
    ② 取種群個體數目為120，產生初始種群。
    ③ 適應度計算：采用懲罰函數法處理約束條件，懲罰因子取0.8，并由目標函數及約束條件得到F(x)。
④ 選擇運算：把當前種群中適應度高的個體按輪盤賭選擇方法遺傳到下一代中，適應度高的個體有更多的機會遺傳到下一代中。根據個體適應度確定其繁殖后在交配池中所占比例的表達式為：
 
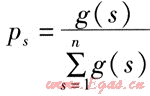
式中ps——在交配池中所占的比例
    g(s)——個體適應度
    n——種群的個數
⑤ 交叉運算：交叉運算是遺傳算法中產生新個體的主要操作過程。由于本文采用實數編碼，因此選用算術交叉，其表達式為：
 
    ⑥ 變異運算：引入變異算子，使遺傳算法具有局部隨機搜索能力，可加速向最優解收斂。本文采用非均勻變異，其優點在于使得最優解搜索過程更加集中在某一最有希望的重點區域中[5]。
   ⑦ 算法終止的條件：采用最大進化代數規則。取最大進化代數為120，當達到此值時就停止運算。
   ⑧ 輸出最優解：對于DN 300、400、500mm直埋水平彎頭，運行20次后的最優解見表1。由表1可知，采用遺傳算法以后，可以準確快速地選擇出合適的最優彎頭，與傳統試算方法相比，提高了設計的效率，降低了彎頭規格，從而降低了工程造價。
表1 運行20次后的最優解
公稱直徑/mm
遺傳算法優化結果
傳統彎頭設計參數
曲率半徑/m
彎頭壁厚/mm
曲率半徑/m
彎頭壁厚/mm
300
2.2
6.4
2.4
9.0
400
2.1
6.4
2.4
9.0
500
1.2
7.2
1.5
10.0
4 結論
    應用遺傳算法對復雜的直埋水平彎頭進行優化設計，由傳統的應力驗算改為優化計算，在設計理念上有了革新，使工程設計更加準確、快捷，該算法在這一領域里有著更加廣闊的應用前景。但需要說明的是，由于合適的遺傳算子是通過不斷實驗選取的，因此一般需經過實驗確定算法中的一些參數才能達到最好的效果，這給實際應用帶來了不便，有待進一步研究。
參考文獻：
[1] 張小趁，陳紅旗，孫云普.直埋供熱管道彎頭的殼體應力分析[J].哈爾濱工業大學學報，2003，(11)：1369-1371.
[2] 劉斯嘉，江楠，甑亮.大型90°彎頭應力測定與爆破試驗研究[J].化工設備與管道，2008，(5)：47-50.
[3] CJJ/T 81—98，城鎮直埋供熱管道工程技術規程[S].
[4] 王飛，張建偉.直埋供熱管道工程設計[M].北京：中國建筑工業出版，2007.
[5] 玄光男，程潤偉.遺傳算法與工程設計[M].北京：科學出版社，2000.
[6] 李敏強，寇紀松，林丹，等.遺傳算法的基本理論與應用[M].北京：科學出版社，2002.
[7] CARLOS A，COELLO C. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms：a survey of the state of the art[J].Computer Methods in Applied Mechanics and Engineering，2002，(191)：1245-1287.
 
(本文作者：王春香 郭曉妮 內蒙古科技大學 機械工程學院 內蒙古包頭 014010)